Plots of spherical harmonic functions of degree 1,2,3

Here are the plots of displacement fields due to spherical harmonics of degree 1, 2 and 3. Displacement is defined as r D(z)

D₁(z) = a * cos z

D₂(z) = a * ( 3/2 cos² z - 1/2)

D₃(z) = a * ( 5/2 cos³ z - 3/2 cos z )

At this plots z is the angle between the upward direction and the radius-vector of the point, a=0.3

Spherical harmonic functions of degree 1

Spherical harmonic functions of degree 2

Spherical harmonic functions of degree 3

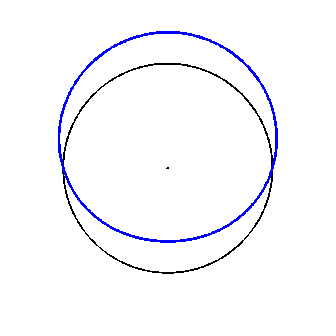
Another example. Three plots are shown here:

black -- orginal, underformed surface
blue -- field of displacements D₁(z) = 0.33 * cos z
red -- the sphere shifted up at 0.33

Ths example demonstrates that the displacements of the degree-1 harmonic does change the shape of the surface: the red and blue curves are different. This transformation changes the distance between the points on the serface.

Back to Leonid Petrov's Home Page.

Last update: 08-JUL-2002 19:19:58